Class 11 Physics Chapter 3 Hindi Medium
सरल रेखा में गति (Motion in a Straight Line)
गति
(Motion): समय के साथ साथ जब कोई वस्तु अपने परिवेश के सापेक्ष अपनी स्थिति में परिवर्तन करती है तो वह
वस्तु गतिशील कहलाती है।
विराम
अवस्था (Rest): समय के साथ साथ जब कोई
वस्तु अपने परिवेश के सापेक्ष अपनी स्थिति
में परिवर्तन नहीं करती है तो वह वस्तु विराम अवस्था में होती है।
निर्देश
तंत्र (frame of reference)
किसी कण की स्थिति को
दर्शाने के लिए हमें एक निर्देश तंत्र की आवश्यकता होती है।
इसके लिए एक समकोणिक
निर्देशांक-निकाय जिसमें तीन परस्पर लम्बवत अक्ष होते हैं जिन्हें x, y- तथा z-अक्ष कहते हैं। समय
नापने के लिए इस निकाय में एक घड़ी रख देते हैं। घड़ी सहित इस निर्देशांक-निकाय को
निर्देश तंत्र (frame of reference) कहते हैं।
जब किसी वस्तु के एक
या अधिक निर्देशांक समय के साथ परिवर्तित होते हैं तो वस्तु को गतिमान कहते हैं।
अन्यथा वस्तु को उस निर्देश तंत्र के सापेक्ष विरामावस्था में मानते हैं।
विरामावस्था
(rest) और गति (motion), सापेक्ष अवस्थायें हैं-
एक वस्तु, एक ही समय में, गति और विराम दोनों अवस्थाओं में हो
सकती है। उदाहरण के लिये, गतिशील ट्रेन में बैठा एक व्यक्ति
उसी ट्रेन में बैठे दूसरे व्यक्ति के सापेक्ष विरामावस्था में है परन्तु पृथ्वी पर
खड़े व्यक्ति के सापेक्ष वह गतिशील है।
यांत्रिकी
(Mechanics)
वस्तुओं की निम्न वेगों पर व्यवस्थित गति के अध्ययन से
सम्बन्धित भौतिकी की शाखा को यांत्रिकी (Mechanics) कहते
हैं।
यांत्रिकी को निम्नलिखित तीन शाखाओं में वर्गीकृत कर सकते
हैं -
(1) स्थैतिकी (Statics)- इस
शाखा के अन्तर्गत विरामावस्था में स्थित वस्तुओं का अध्ययन किया जाता है।
(2) शुद्ध गति विज्ञान (kinematics)- में वस्तुओं की केवल गति का अध्ययन करते हैं, गति के
कारणों का नहीं।
(3) गति
विज्ञान (dynamics) -में
वस्तुओं की गति के साथ-साथ गति के कारणों का भी अध्ययन करते हैं।
गति के प्रकार (Types
of Motion)
1.
एक-विमीय गति
(One Dimensional Motion)
2.
द्वि-विमीय गति
(Two Dimensional Motion)
3.
त्रि-विमीय गति (Three
Dimensional Motion)
(1)
एक-विमीय गति (One Dimensional Motion)- यदि समय के साथ केवल एक निर्देशांक
परिवर्तित होता है तो गति एक-विमीय गति (1 - D) या सरल
रेखीय गति कहलाती है। जैसे- ऊर्ध्वाधर ऊपर की ओर फेंकी गयी वस्तु की गति, एक सीधी पटरी पर रेलगाड़ी की गति, सिलाई मशीन की सुई
की गति।
(2)
द्वि-विमीय गति (Two Dimensional Motion)-
यदि समय के साथ केवल दो निर्देशांक परिवर्तित होते है, तो गति द्वि-विमीय (2 – D) या समतल में गति कहलाती
है। जैसे – कैरम बोर्ड पर गोटी (carom coin) की गति, सूर्य के चारों ओर पृथ्वी की परिक्रमण गति, ,
मैदान में क्रिकेट खेलते खिलाड़ी की गति।
(3)
त्रि-विमीय गति (Three Dimensional Motion)-
यदि समय के साथ तीनों निर्देशांक परिवर्तित होते है, तो
गति त्रि-विमीय (3 - D) या आकाश में गति कहलाती है। आसमान
में उड़ते पक्षी की गति, हवाई जहाज की गति।
गति
के अन्य प्रकार
1.
स्थानान्तरीय (translatory)
2.
घूर्णी (rotatory)
3.
दोलनी (oscillatory)
स्थानान्तरीय
गति (Translatory Motion) -
स्थानान्तरीय गति एक सरल रेखा या वक्र-पथ (curved path) के
अनुदिश हो सकती है। जैसे- किसी सिथर वस्तु के सापेक्ष एक कार की गति।
घूर्णन
गति (Rotational Motion)- जब
कोई दृढ़ पिण्ड किसी स्थिर अक्ष के परितः घूर्णन करता है तब पिण्ड की गति घूर्णन
गति कहलाती है। जैसे-छत के पंखे की गति।
दोलन
या कम्पन गति (Oscillatory or Vibrational
Motion)- जब कोई कण अपनी माध्य स्थिति के इर्द-गिर्द
अपनी गति को निश्चित समयान्तराल में दोहराता है तब कण की गति दोलन या कम्पन गति
कहलाती है। जैसे दीवार घड़ी के लोलक की गति, स्प्रिंग से
जुड़े द्रव्यमान की गति आदि।
अदिश
व सदिश राशियाँ (Scalar and Vector Quantities)
अदिश
राशियाँ (Scalar Quantities)- वे भौतिक राशियाँ जिन्हें व्यक्त करने के लिए केवल परिमाण की आवश्यकता
होती है, दिशा की नहीं, अदिश कहलाती
है। उदाहरण : दूरी, द्रव्यमान, समय,
चाल, घनत्व, आयतन,
तापमान, विद्युत धारा आदि।
सदिश
राशियाँ (Vector Quantities)- वे भौतिक राशियाँ जिन्हें पूर्णतया व्यक्त करने के लिए परिमाण के साथ एक
निश्चित दिशा की भी आवश्यकता होती है, सदिश राशि कहलाती हैं।
उदाहरण : विस्थापन, वेग, त्वरण,
बल इत्यादि।
सदिश
राशि का निरूपण(Representation of Vectors):
सदिश को एक सरल रेखा के सिरे पर तीर का निशान लगाकर निरूपित करते हैं। इसकी लम्बाई
उसके परिमाण के समानुपाती होती है।
महत्वपूर्ण बिन्दु :
चाल = धनात्मक
तथा नियत
tan θ = -ve तथा स्थिर
चाल = ऋणात्मक तथा नियत
याद
रहे किं x-अक्ष से 90° से अधिक कोण पर झुकी सरल रेखा ऋणात्मक वेग को निरूपित करती है।
(i) यदि ग्राफ,
BC द्वारा दर्शायी गयी, समय-अक्ष के समान्तर
एक सरल रेखा है, तो इसका अर्थ है कि पिण्ड नियत वेग से
गतिशील है या त्वरण शून्य (a =0) है। |
v-t
ग्राफ का ढाल = tanq
दूरी
और विस्थापन (Distance and Displacement)
दूरी
(Distance) :
किसी पिंड द्वारा
निश्चित समय में तय किए गए पथ की लम्बाई को दूरी कहते हैं।
·
यह अदिश राशि है।
·
दूरी को ओडोमीटर द्वारा मापा
जाता है।
·
दूरी का मात्रक: मीटर (SI) तथा cm (CGS)।
·
विमीय सूत्र : [M0L1T0]
·
दूरी कभी ऋणात्मक नहीं हो
सकती।
विस्थापन
(Displacement)
किसी पिंड की
प्रारम्भिक (initial) तथा अन्तिम (final) स्थितियों के बीच की दिशात्मक दूरी को कण का विस्थापन कहते हैं।
· यह
सदिश राशि है।
·
विस्थापन का मात्रक: मीटर (SI) तथा cm (CGS)।
·
विस्थापन धनात्मक, शून्य या ऋणात्मक हो सकता है।
·
विमीय सूत्र : [M0L1T0]
· दो
निश्चित बिन्दुओं के मध्य अनन्त दूरियाँ सम्भव होती है क्योंकि दो निश्चित
बिन्दुओं के मध्य अनन्त पथ सम्भव है। दो दिये गये बिन्दुओं के मध्य विस्थापन का
केवल एक मान सम्भव है।
· यदि
कोई वस्तु एक सरल रेखा के अनुदिश बिना दिशा बदले गति करती है तो –
दूरी = |विस्थापन। = विस्थापन का परिमाण
अन्यथा दूरी
> विस्थापन ।
प्रश्न:
यदि
एक व्यक्ति 10 मीटर उत्तर की ओर तथा 20
मीटर पूर्व की ओर जाता है, तब उसका विस्थापन
होता है
(a) 22.5 m ।
(b)
25 m
(c)
25.5 m
(d)
30 m।
विस्थापन से दूरी के अनुपात का आंकिक मान (numerical
value) होता है :
(a)
सदैव एक से कम
(b) सदैव एक के बराबर
(c) सदैव एक से अधिक
(d) एक के बराबर अथवा कम
बिन्दु
वस्तु (Point Objects):
यदि कोई वस्तु अपने आमाप की तुलना में बहुत अधिक दूरी तय
करती है तो वह वस्तु बिन्दु वस्तु कहलाती है।
जैसे: जब कोई कार कुछ किलोमीटर की दूरी तय करती है तो उसे
बिन्दु वस्तु माना जा सकता है।
इसी तरह, जब पृथ्वी सूर्य के
चारों ओर परिक्रमा करती है तो उसे भी बिन्दु वस्तु माना जा सकता है।
चाल
व वेग (Speed and Velocity)
चाल :- इकाई समय में
तय की गई दूरी को चाल कहते हैं।
अथवा
समय के साथ दूरी में परिवर्तन की दर को चाल कहते हैं।
·
मात्रक = मीटर/सेकण्ड (S.I.), सेमी/सेकण्ड (C.G.S.)
·
विमा = [M0 L T-1 ]
·
चाल एक अदिश राशि है।
नोट :- गतिमान कण के लिये चाल कभी शून्य अथवा ऋणात्मक नहीं
हो सकती है सदैव धनात्मक होती है। |
चाल के प्रकार (Types of
Speed)
एकसमान
चाल (Uniform Speed or Constant Speed)
: जब कोई गतिमान पिंड समान समयान्तराल में समान दूरी तय करता है तो उसकी चाल
एकसमान चाल कहलाती है।
असमान
चाल या परिवर्ती चाल (Variable Speed): यदि
कोई गतिमान कण समान समयान्तरालों में असमान दुरियाँ तय करता है तो उसकी चाल असमान
या परिवर्ती चाल कहलाती है।
औसत
चाल (माध्य चाल) (Average speed) : वस्तु द्वारा तय की गई कुल दूरी और उसमें लगे कुल समय के अनुपात को औसत
चाल कहते हैं।
तात्क्षणिक
चाल (Instantaneous speed)
समय के विशेष क्षण पर
कण की चाल तात्क्षणिक चाल कहलाती है।
वाहनों के स्पीडोमीटर
तात्क्षणिक चाल मापते हैं।
औसत
चाल को किसी समयान्तराल के लिये परिभाषित किया जाता है, जबकि तात्कालिक चाल को किसी एक क्षण के लिये परिभाषित किया जाता है।
वेग
(Velocity):
समय के सापेक्ष विस्थापन में परिवर्तन की दर वेग कहलाती
है।
· वेग
एक सदिश राशि है।
· विमा
: [M0 L T-1 ]
· मात्रक
: मीटर / सैकण्ड (S.I.), सेमी /
सेकण्ड (C.G.S.)
· वेग
धनात्मक,
ऋणात्मक तथा शून्य हो सकता है।
· वेग
की दिशा सदैव विस्थापन की दिशा में होती है।
वेग के प्रकार
(Types of Velocity)
एकसमान
वेग (Uniform Velocity) -
जब कण के वेग को परिमाण तथा दिशा दोनों समय के साथ परिवर्तित ना हो तो उसका वेग
एकसमान वेग कहलाता है। ऐसा केवल तभी सम्भव है जब कण एक सरल रेखा में बिना दिशा
परिवर्तित किये गति करे।
असमान
या परिवर्ती वेग (Non-Uniform Velocity) -
जब वेग का परिमाण अथवा दिशा या दोनों समय के साथ परिवर्ती हो तो कण का वेग असमान
वेग या परिवर्ती वेग कहलाता है।
औसत
वेग (Average velocity): गतिमान
कण द्वारा तय किये गये कुल विस्थापन और उसमें लगे कुल समय के अनुपात को औसत वेग
कहते हैं।
तात्क्षणिक
वेग(Instantaneous Velocity):
समय के विशेष क्षण पर कण का वेग उसका तात्क्षणिक वेग कहलाता है।
NOTE:
ü यदि
कोई पिण्ड नियत वेग से गति कर रहा है, तो औसत वेग
तथा तात्कालिक वेग बराबर होते हैं। वेग धनात्मक या ऋणात्मक हो सकती है, क्योंकि यह एक सदिश है, परन्तु चाल कभी ऋणात्मक नहीं
हो सकती, क्योंकि यह वेग का परिमाण है।
ü किसी
गतिशील पिण्ड के औसत वेग की दिशा हमेशा विस्थापन के अनुदिश होती है लेकिन
तात्क्षणिक वेग की दिशा हमेशा पथ के स्पर्श रेखीय होती है।
ü यदि
कोई वस्तु एक सरल रेखा के अनुदिश बिना दिशा बदले गति करती है तो औसत वेग का परिमाण
औसत चाल के बराबर होता है, अन्यथा, औसत |< औसत ।
ü यदि
कोई पिण्ड नियत चाल से गतिमान है तो उसका वेग नियत (constant)
हो भी सकता है और नहीं भी। एकसमान वृत्तीय गति में, यद्यपि चाल नियत रहती है किन्तु दिशा बदलते रहने के कारण प्रति क्षण वेग
बदल जाता है।
ü किसी
पिण्ड के लिये, गति के दौरान किसी क्षण पर, विस्थापन शून्य तथा वेग परिमित (finite) हो सकते हैं
(जैसे--किसी सरल आवर्त गति के साम्यावस्था में)। साथ ही, किसी
पिण्ड के लिये, गति के दौरान किसी क्षण पर, विस्थापन परिमित तथा वेग शून्य हो सकता है।
प्रश्न: कोई कार एक
सरल रेखा (मान लीजिए चित्र 3.1 में रेखा OP) के अनुदिश गतिमान है । कार 0 से चलकर 18 s में P तक पहुंचती है, फिर 6.0
s में स्थिति Q पर वापस आ जाती है। कार के औसत
वेग एवं औसत चाल की गणना कीजिए, जब (a) कार 0 से P तक जाती है,
और (b) जब वह 0 से P
तक जा कर पुनः Q पर वापस आ जाती है ।
प्रश्न: एक वाहन किसी
दूरी के आधे भाग को चाल v1 से
तथा अन्य आधे भाग को v2 चाल के साथ तय करता है। तब इसकी औसत चाल होगी
प्रश्न: एक कार एक
सीधी सड़क के अनुदिश पहले आधे समय में v1
वेग से तथा दूसरे आधे समय में v2 वेग
से चलता है। कार का माध्य वेग (mean velocity) होगा :
एक वस्तु प्रथम एक-तिहाई
दूरी वेग v1 से, दूसरी एक-तिहाई दूरी वेग v2,
से तथा शेष दूरी वेग v3 से
तय करती है। औसत वेग है :
Q.
एक वस्तु प्रथम एक-तिहाई दूरी 20 मी/से के वेग
से, दूसरी एक-तिहाई दूरी 30 मी/से के
वेग से तथा अन्तिम एक-तिहाई दूरी 40 मी/से के वेग से तय करती
है। औसत वेग लगभग होगा :
(A) 28 मी/से
(B)
38 मी/से
(C) 18 मी/से
(D)
8 मी/से
Q.
किसी कार का गतिमापी मापता है
(A) औसत चाल (B) औसत वेग (C) तात्क्षणिक
चाल (D) तात्क्षणिक वेग
Q. 20 मीटर की
त्रिज्या वाले एक वृत्तीय मार्ग पर एक साइकिल चालक आधे चक्कर को 20 सेकण्ड में पूरा कर लेता है। इसका औसत वेग है
(A) शून्य
(B)
4πm/s
(C)
2 ms-1
(D)
8 π ms/
त्वरण
(Acceleration):
इकाई समय में वेग में परिवर्तन की दर को त्वरण कहते हैं।
अथवा
किसी वस्तु के वेग में परिवर्तन की दर को त्वरण कहते हैं ।
· यह
एक सदिश राशि है।
· विमा
: [M0
L1 T-2 ]
· मात्रक
: m/s2
[SI पद्द्ति] , cm/s2 [CGS पद्द्ति]
त्वरण के प्रकार (Types
of Acceleration)
एकसमान
त्वरण (Uniform Acceleration):
जब त्वरण का परिमाण
तथा दिशा दोनों नियत रहते हैं तो ऐसे त्वरण को एकसमान त्वरण कहते हैं।
असमान
त्वरण (Non-uniform Acceleration / Variable Acceleration):
जब त्वरण का परिमाण
अथवा दिशा अथवा दोनों किसी अन्य भौतिक राशि के सापेक्ष परिवर्ति हो तो इसे
परिवर्ती या असमान त्वरण कहते हैं।
औसत
त्वरण (Average Acceleration) :
औसत त्वरण कुल वेग
में परिवर्तन तथा कुल समय का अनुपात होता है।
तात्क्षणिक
त्वरण (Instantaneous Acceleration):
समय के विशेष क्षण पर
कण का त्वरण तात्क्षणिक त्वरण कहलाता है।
त्वरण एक सदिश राशि है, यह धनात्मक, ऋणात्मक या शून्य हो सकता है।
(i) यदि वस्तु सरल रेखा के
अनुदिश समान वेग से गति करती है तो त्वरण शून्य होगा।
(ii)
यदि एक वस्तु सरल रेखा के अनुदिश बढ़ते हुए वेग से गति करती है। |
तो त्वरण की दिशा गति की दिशा के अनुदिश होती है तथा त्वरण धनात्मक
होता है।
(iii) यदि वस्तु सरल रेखा के
अनुदिश घटते हुए वेग से गति करती है तो त्वरण की दिशा गति की दिशा के विपरीत होती
है तथा त्वरण ऋणात्मक होता है।
Important
Points:
·
एक पिण्ड शून्य वेग के होते
हुए भी त्वरणयुक्त हो सकता है,
उदाहरण-1
ऊपर की ओर प्रक्षेपित किसी पिण्ड के उच्चतम बिन्दु पर वेग शून्य होता है तथा त्वरण
गुरुतवीय त्वरण (g) के बराबर होता है।
उदाहरण-2
सरल आवर्त गति में चरम स्थिति (extreme position) पर।
·
जब कण वक्रीय पथ पर एकसमान
चाल से गतिमान हो तो उस पर त्वरण क्रियाशील (Non-zero)
होता हैं। उदाहरण :- जब कोई पिण्ड एकसमान चाल से वृत्तीय गति करता है तो उसका वेग दिशा
बदलते रहने के कारण निरन्तर बदलता रहता है। प्रति एकांक समय में हुए इस प्रकार के
वेग परिवर्तन को अभिलम्ब त्वरण (normal acceleration) कहते
हैं जिसकी दिशा सदैव वेग की दिशां के लम्बवत् होती है।
·
जब कोई कण परिवर्ती चाल से
गतिमान हो तो उस पर आवश्यक रूप से त्वरण क्रियाशील (Non-zero) होता है।
·
यदि त्वरण नियत है तो त्वरण
एकसमान रहता है परन्तु गति असमान होती है और यदि त्वरण नियत नहीं है तो त्वरण व
गति दोनों असमान होते हैं।
·
किसी पिण्ड का वेग परिमाण व
दिशा दोनों में परिवर्ती (varying) होने पर भी उसका त्वरण
नियत हो सकता है। जैसे, प्रक्षेप्य,गति
की स्थिति में, वेग को परिमाण व दिशा दोनों बदलते रहते हैं
परन्तु त्वरण ‘g नियत रहता है।
प्रश्न: उदाहरण सहित
निम्नलिखित के बीच के अंतर को स्पष्ट कीजिए :
(a) किसी समय अंतराल में विस्थापन के परिमाण (जिसे कभी-कभी दूरी भी कहा जाता
है) और किसी कण द्वारा उसी अंतराल के दौरान तय किए गए पथ की कुल लंबाई ।
(b) किसी समय अंतराल में औसत वेग के परिमाण और उसी अंतराल में औसत चाल (किसी
समय अंतराल में किसी कण की औसत चाल को समय अंतराल द्वारा विभाजित की गई कुल
पथ-लंबाई के रूप में परिभाषित किया जाता है) ।
प्रदर्शित कीजिए कि (a) व (b) दोनों में ही दूसरी राशि पहली से अधिक या उसके
बराबर है । समता का चिह्न कब सत्य होता है ? (सरलता के लिए
केवल एकविमीय गति पर विचार कीजिए ।)
प्रश्न: कोई व्यक्ति
अपने घर से सीधी सड़क पर 5 km h-1 की चाल से 2.5
km दूर बाजार तक पैदल चलता है । परंतु बाजार बंद देखकर वह उसी क्षण
वापस मुड़ जाता है तथा 7.5 km h-1 की चाल से घर
लौट आता है। समय अंतराल (i) 0 - 30 मिनट, (ii) 0 - 50
मिनट, (iii) 0 - 40 मिनट की अवधि में उस
व्यक्ति (a) के माध्य वेग का परिमाण, तथा
(b) का माध्य चाल क्या है?
प्रश्न: हमने अभ्यास 3.13
तथा 3.14 में औसत चाल व औसत वेग के परिमाण के
बीच के अंतर को स्पष्ट किया है । यदि हम तात्क्षणिक चाल व वेग के परिमाण पर विचार
करते हैं तो इस तरह का अंतर करना आवश्यक नहीं होता । तात्क्षणिक चाल हमेशा
तात्क्षणिक वेग के बराबर होती है । क्यों ?
गति
का आलेखीय निरूपण (Graphical Representation of
Motion)
स्थिति-समय
आलेख (Position-Time Graph) :
गतिशील वस्तु की
विभिन्न क्षणों पर स्थितिं तथा उसके संगत समय के मध्य खींचा गया आलेख, स्थिति समय आलेख कहलाता है।
स्थिति-समय
आलेख जब कण विराम अवस्था हो :
यदि जब कण विराम अवस्था
हो विस्थापन-समय ग्राफ़ समय- अक्ष के समानांतर एक
सीधी रेखा होगा जैसा कि चित्र में दर्शाया गया है।
स्थिति-समय
आलेख जब कण एक समान वेग से गतिमान हो :
समान वेग से गतिमान
कण में समान समय अंतराल में समान विस्थापन होता है। इसलिए, समान वेग से गतिमान कण के लिए विस्थापन-समय ग्राफ़ समय-अक्ष पर झुकी एक सीधी रेखा होगा जैसा कि चित्र में दर्शाया गया है।
विस्थापन-समय
ग्राफ़ से वेग ज्ञात करना :
समान वेग से गतिमान
कण के लिए विस्थापन-समय ग्राफ़ समय-अक्ष पर झुकी
एक सीधी रेखा होगा जैसा कि चित्र में दर्शाया गया है।
ग्राफ पर दो बिन्दुओं
क्रमश: A
व B के लिए माना वस्तु का समय t1 पर विस्थापन S1 है तथा समय t2
पर विस्थापन S2 है।
ग्राफ का ढाल वस्तु
के वेग को प्रदर्शित करता है।
यदि ग्राफ का ढाल = 0
x-अक्ष पर झुकी हुई सरल रेखा (straight line) यह
दर्शाती हैं कि पिण्ड नियत वेग से गतिमान है।
हो तो ,
+ve तथा स्थिर
वेग-समय
ग्राफ (Velocity-Time Graph):
(A) यदि कण
एकसमान वेग से गतिमान हो तो :
एकसमान वेग से गतिमान
कण के लिए यदि हम वेग-समय ग्राफ खींचे तो यह समय-अक्ष के समांतर एक सीधी रेखा होगी, जैसा कि चित्र में दर्शाया गया है।
B) यदि कण एक
समान त्वरण से गतिमान हो:
एक कण को एकसमान
त्वरण से गतिमान कहा जा सकता है यदि इसका वेग समान समय अंतराल में समान रूप से
बदलता रहे।
एकसमान त्वरण से
गतिमान कण के लिए वेग-समय ग्राफ समय अक्ष पर झुकी एक सरल रेखा होगी, जिसका एक उदाहरण चित्र में दर्शाया गया है।
वेग
समय ग्राफ के बारे में अन्य महत्वपूर्ण जानकारी :
(ii) यदि
ग्राफ -अक्ष पर झुकी धनात्मक ढाल (slope) वाली एक सरल रेखा (ग्राफ
OA) है तो इसका अर्थ है कि पिण्ड नियत त्वरण (a = स्थिर) से गति कर रहा है।
(iii) यदि
ग्राफ x-अक्ष पर झुकी ऋणात्मक ढाल वाली. एक ऋजु रेखा
(ग्राफ FG) है तो इसका अर्थ है पिण्ड की गति
मन्दन (retardation) के अन्तर्गत है।
(iv)
कोई भी वेग-समय ग्राफ समय-अक्ष के लम्बवत् नहीं हो सकता । क्योंकि
यह अनन्त त्वरण को प्रकट करता है।
(v) ग्राफ OD बढ़ते हुए त्वरण को प्रदर्शित करता है।
(vi) ग्राफ OE घटते हुए त्वरण को प्रदर्शित करता है।
वेग-समय
(Velocity-time) ग्राफ के लाभ :
(1)
v-t ग्राफ का ढाल:
= त्वरण
अत: v-t
ग्राफ का ढाल = त्वरण
(2)
वेग-समय ग्राफ व समय अक्ष के बीच घिरा क्षेत्रफल
वेग-समय ग्राफ व समय
अक्ष के बीच घिरा क्षेत्रफल
=
ar(OACD) + ar(ABC)
= OA×OD
+
1/2(AC
× BC)
=
ut + 1/2(
अत: वेग-समय ग्राफ व समय
अक्ष के बीच घिरा क्षेत्रफल = विस्थापन
प्रश्न 3.3
: एक महिला अपने घर से प्रातः 9.00 बजे 2.5
km दूर अपने कार्यालय के लिए सीधी सड़क पर 5 km h-1
चाल से चलती है । वहाँ वह सायं 5.00 बजे तक
रहती है और 25 km h-1 की चाल से चल रही किसी ऑटो
रिक्शा द्वारा अपने घर लौट आती है । उपयुक्त पैमाना चुनिए तथा उसकी गति का x
- t ग्राफ खींचिए ।
उत्तर:
प्रश्न 3.4 : कोई शराबी किसी तंग गली में 5 कदम आगे बढ़ता है
और 3 कदम पीछे आता है, उसके बाद फिर 5
कदम आगे बढ़ता है और 3 कदम पीछे आता है,
और इसी तरह वह चलता रहता है । उसका हर कदम 1m लंबा
है और 1s समय लगता है। उसकी गति का x - t ग्राफ खींचिए । ग्राफ से तथा किसी अन्य विधि से यह ज्ञात कीजिए कि वह जहां
से चलना प्रारंभ करता है वहाँ से 13 m दूर किसी गड्ढे में
कितने समय पश्चात गिरता है ।
उत्तर: प्रथम 8s
में गड्ढे की दिशा में विस्थापन = 5m - 3m
= 2m
2m
विस्थापन में लगा समय = 8s
8m
विस्थापन में लगा समय =
32s के
बाद अगले 5m चलने में लगा समय = 5s
इसलिए, शराबी को गड्ढे में गिरने में लगा समय = 32s + 5s
=37s
प्रश्न: चित्र 3.20
में (a) से (d) तक के
ग्राफों को ध्यान से देखिए और देखकर बताइए कि इनमें से कौन-सा ग्राफ एकविमीय गति
को संभवतः नहीं दर्शा सकता ।
प्रश्न: चित्र 3.21
में किसी कण की एकविमीय गति का x- t ग्राफ दिखाया
गया है। ग्राफ से क्या यह कहना ठीक होगा कि यह कण t<0 के
लिए किसी सरल रेखा में और t>0 के लिए किसी परवलीय पथ में
गति करता है । यदि नहीं, तो ग्राफ के संगत किसी उचित भौतिक
संदर्भ का सुझाव दीजिए ।
प्रश्न: चित्र में दिखाए गए प्रत्येक ग्राफ के लिए किसी उचित
भौतिक स्थिति का सुझाव दीजिए:
प्रश्न: चित्र में किसी कण की एकविमीय सरल आवर्ती गति के लिए x
- t ग्राफ दिखाया गया है । (इस गति के बारे में आप अध्याय 14
में पढ़ेंगे) समय t = 0.3 s, 1.2s, -1.2s पर
कण के स्थिति, वेग व त्वरण के चिह्न क्या होंगे?
प्रश्न: चित्र किसी कण
की एकविमीय गति का x – t ग्राफ दर्शाता है ।
इसमें तीन समान अंतराल दिखाए गए हैं । किस अंतराल में औसत चाल अधिकतम है और किसमें
न्यूनतम है ? प्रत्येक अंतराल के लिए औसत वेग का चिह्न
बताइए।
प्रश्न: चित्र में किसी नियत (स्थिर) दिशा के अनुदिश चल रहे कण
का चाल-समय ग्राफ दिखाया गया है । इसमें तीन समान समय अंतराल दिखाए गए हैं । किस
अंतराल में औसत त्वरण का परिमाण अधिकतम होगा ? किस
अंतराल में औसत चाल अधिकतम होगी? धनात्मक दिशा को गति की
स्थिर दिशा चुनते हुए तीनों अंतरालों में v तथा a के चिह्न बताइए । A, B, C, व D बिंदुओं पर त्वरण क्या होंगे ?
एकसमान त्वरण से गतिमान वस्तु का
शुद्धगतिकी संबंधी समीकरण :
ग्राफ़ीय
विधि द्वारा एकसमान त्वरण से गतिमान वस्तु के समीकरणों की उत्पत्ति
माना एक वस्तु एक
सीधी रेखा में एक समान त्वरण a से
गतिमान है। इसका प्रारम्भिक वेग u तथा
समय t
पर वेग v है। यदि हम इस वस्तु के लिए
वेग-समय ग्राफ खीचे तो यह ग्राफ समय अक्ष पर झुकी एक सरल रेखा होगी।
उपर्युक्त वेग-समय ग्राफ
से –
(iv) n वीं सेकेंड में वस्तु द्वारा तय दूरी:
उत्पत्ति :
समाकलन
विधि द्वारा एकसमान त्वरण से गतिमान वस्तु के समीकरणों की उत्पत्ति:
(i)
v=u+at की
उत्पत्ति :
त्वरण की परिभाषा से-
दोनों तरफ समाकलन करने
पर-
(ii) s = ut + 1/2
दोनों तरफ समाकलन करने
पर –
(iii) v2-u2 = 2as
प्रश्न 3.6: सीधे राजमार्ग पर कोई कार 126
km h-1 की चाल से चल रही है । इसे 200 m की दूरी पर रोक दिया जाता है । कार के मंदन को एकसमान मानिए और इसका मान
निकालिए । कार को रुकने में कितना समय लगा?
प्रश्न: दो
रेलगाड़ियाँ A व B दो समांतर
पटरियों पर 72 km h-1 की एकसमान चाल से एक ही
दिशा में चल रही हैं। प्रत्येक गाड़ी 400 m लंबी है और गाड़ी
A गाड़ी B से आगे है । B का चालक A से आगे निकलना चाहता है तथा lm s-2
से इसे त्वरित करता है । यदि 50 s के बाद B
का गार्ड A के चालक से आगे हो जाता है तो
दोनों के बीच आरंभिक दूरी कितनी थी?
प्रश्न: कोई
खिलाड़ी एक गेंद को ऊपर की ओर आरंभिक चाल 29 m s-1 से फेंकता है,
(i)
गेंद की ऊपर की ओर गति के दौरान त्वरण की दिशा क्या होगी?
(ii)
इसकी गति के उच्चतम बिंदु पर गेंद के वेग व त्वरण क्या होंगे?
(iii)
गेंद के उच्चतम बिंदु पर स्थान व समय को x = 0 व t = 0 चुनिए, ऊर्ध्वाधर नीचे
की ओर की दिशा को x-अक्ष की धनात्मक दिशा मानिए । गेंद की
ऊपर की व नीचे की ओर गति के दौरान स्थिति, वेग व त्वरण के
चिह्न बताइए।
(iv) किस ऊँचाई तक गेंद ऊपर जाती
है और कितनी देर के बाद गेंद खिलाड़ी के हाथों में आ जाती है ?
[g
= 9.8 m s-2 तथा वायु का प्रतिरोध नगण्य है ।
प्रश्न: नीचे दिए
गए कथनों को ध्यान से पढ़िए और कारण बताते हुए व उदाहरण देते हुए बताइए कि वे सत्य
हैं या असत्य, एकविमीय गति में किसी कण की
(a) किसी क्षण चाल शून्य होने पर
भी उसका त्वरण अशून्य हो सकता है ।
(b) चाल शून्य होने पर भी उसका
वेग अशून्य हो सकता है ।
(c) चाल स्थिर हो तो त्वरण अवश्य
ही शून्य होना चाहिए ।
(d) चाल अवश्य ही बढ़ती रहेगी,
यदि उसका त्वरण धनात्मक हो ।
प्रश्न: किसी गेंद
को 90
m की ऊँचाई से फर्श पर गिराया जाता है । फर्श के साथ प्रत्येक टक्कर
में गेंद की चाल 1/10 कम हो जाती है । इसकी गति का t
= 0 से 12s के बीच चाल-समय ग्राफ खींचिए ।
आपेक्षिक
वेग :
किसी वस्तु के
सापेक्षदूसरी वस्तु का आपेक्षिक वेग वह दर है जिससे कि पहली वस्तु के सापेक्ष
दूसरी वस्तु की स्थिति बदलती है।
यदि वस्तु A और B
के वेग क्रमश: VA तथा VB
हों तो
A
के सापेक्ष B का आपेक्षिक वेग, VAB = VA –VB
B
के सापेक्ष A का आपेक्षिक वेग, VAB = VA –VB
अत: VAB = –VBA
कुछ
विशेष परिस्थितियाँ :
(a) यदि VA = VB
, तब VAB = VA
–VB =0 , इस स्थिति में दोनों
वस्तुएँ एक दूसरे से सदैव स्थिर दूरी पर रहती हैं और उनके स्थिति-समय ग्राफ परस्पर
समांतर रेखाएँ होती हैं।
(b) VA > VB , तब VAB = VA –VB = +ve तथा VBA = VB –VA= -ve होगी। इस स्थिति में एक वस्तु के ग्राफ का ढाल
दूसरी वस्तु के ग्राफ के ढाल की अपेक्षा अधिक होता है। दोनों ग्राफ एक उभयनिष्ठ
बिन्दु पर मिलते हैं। इस बिन्दु से हमें t व x
के जो मान प्राप्त होते हैं उनसे हमें उस क्षण व स्थिति का पता
चलता है जिस पर दोनों वस्तुएँ एक दूसरे से मिलती हैं। इस प्रकार इस क्षण पर वस्तु A वस्तु B से आगे निकल जाएगी।
(c) जब दो
वस्तुएँ परस्पर विपरीत दिशाओं में गतिमान हो , इस स्थिति
स्थिति-समय ग्राफ जैसा चित्र में दिखाया गया है ऐसा हो सकता है। इस ग्राफ से दोनों
वस्तुओं के मिलने का समय व स्थिति ज्ञात की जा सकती है।
Numerical (संख्यात्मक प्रश्न)
प्रश्न 3.5:
कोई जेट वायुयान 500
km h-1 की चाल से चल रहा है और यह जेट यान के सापेक्ष 1500
km h-1 की चाल से अपने दहन उत्पादों को बाहर निकालता है।
जमीन पर खड़े किसी प्रेक्षक के सापेक्ष इन दहन उत्पादों की चाल क्या होगी?
माना , वायुयान की दिशा में वेग
ध्नात्मक है।
तथा, दहन उत्पादों (गैस) का वेग = Vg
वायुयान का वेग, Vp = 500 km/h
गैस का वायुयान के सापेक्ष वेग, Vgp = -1500 km/h
Vgp =
Vg –Vp
-1500 = Vg – 500
Vg = -1000 km/h
इसलिए, दहन उत्पादों का जमीन के
सापेक्ष वेग = 1000 km/h होगा तथा इसकी दिशा वायुयान के वेग
की दिशा से विपरीत दिशा में होगी।
प्रश्न: दो-लेन वाली किसी सड़क पर कार A
36 km h-1 की चाल से चल रही है । एक दूसरे की विपरीत
दिशाओं में चलती दो कारें B व C जिनमें
से प्रत्येक की चाल 54 km h-1 है, कार A तक पहुँचना चाहती हैं । किसी क्षण जब दूरी AB
दूरी AC के बराबर है तथा दोनों 1km है, कार B का चालक यह निर्णय
करता है कि कार C के कार A तक पहुँचने
के पहले ही वह कार A से आगे निकल जाए । किसी दुर्घटना से
बचने के लिए कार B का कितना न्यूनतम त्वरण जरूरी है ?
प्रश्न: दो नगर A व B नियमित बस सेवा द्वारा एक दूसरे से जुड़े हैं और प्रत्येक T मिनट के बाद दोनों तरफ बसें चलती हैं। कोई व्यक्ति साइकिल से 20
km/h की चाल से A से B की
तरफ जा रहा है और यह नोट करता है कि प्रत्येक 18 मिनट के बाद
एक बस उसकी गति की दिशा में तथा प्रत्येक 6 मिनट बाद उसके
विपरीत दिशा में गुजरती है । बस सेवाकाल T कितना है और बसें
सड़क पर किस चाल (स्थिर मानिए) से चलती हैं?
प्रश्न: किसी
राजमार्ग पर पुलिस की कोई गाड़ी 30 km/h की चाल से चल रही
है और यह उसी दिशा में 192 km/h की चाल से जा रही किसी चोर
की कार पर गोली चलाती है। यदि गोली की नाल मुखी चाल 150 m s-1 है तो चोर की कार को गोली किस चाल के साथ आघात करेगी ? (नोट : उस चाल को ज्ञात कीजिए जो चोर की कार को हानि पहुँचाने में
प्रासंगिक हो) ।
प्रश्न: नीचे दिए गए गति के कौन से उदाहरणों में वस्तु को
लगभग बिंदु वस्तु माना जा सकता है :
(a) दो स्टेशनों के बीच बिना किसी
झटके के चल रही कोई रेलगाड़ी ।
(b) किसी वृत्तीय पथ पर साइकिल
चला रहे किसी व्यक्ति के ऊपर बैठा कोई बंदर ।
(c) जमीन से टकरा कर तेजी से
मुड़ने वाली क्रिकेट की कोई फिरकती गेंद ।
(d) किसी मेज के किनारे से फिसल
कर गिरा कोई बीकर ।
उत्तर: यहाँ (a) व (b) में वस्तु को बिन्दु वस्तु माना जा सकता है क्योंकि इन दोनों स्थितियों
में वस्तु द्वारा तय दूरी वस्तु के आमाप से काफी अधिक है।
प्रश्न: दो बच्चे A व B अपने विद्यालय O से लौट कर अपने-अपने घर क्रमश: P
तथा Q को जा रहे हैं । उनके स्थिति-समय (x
- t) ग्राफ चित्र 3.19 में दिखाए गए हैं ।
नीचे लिखे कोष्ठकों में सही प्रविष्टियों को चुनिए :
(a) B/A की तुलना में A/B
विद्यालय से निकट रहता है ।
(b) B/A की तुलना में A/B
विद्यालय से पहले चलता है ।
(c) B/A की तुलना A/B तेज चलता है ।
(d) A और B घर (एक ही/भिन्न) समय पर पहुँचते हैं ।
उत्तर: (a) B की तुलना में A
विद्यालय से निकट रहता है ।
(b) A की तुलना में B विद्यालय से पहले चलता है ।
(c) B की तुलना A तेज चलता है ।
(d) A और B घर पर एक ही समय पर पहुँचते हैं ।
Multiple
Choice Questions
1.
एकसमान गति में चलते हुए कण में हो सकता है:
(a)
त्रिज्य (radial) त्वरण
(b) स्पर्श-रेखीय (tangential)
त्वरण
(c) त्रिज्य के स्पर्श-रेखीय,
दोनों त्वरण
(d)
न त्रिज्य, न ही स्पर्श-रेखीय त्वरण
Ans
A
2.
विस्थापन से दूरी के अनुपात का आंकिक मान (numerical value) होता है :
(a) सदैव एक से कम
(b) सदैव एक के बराबर
(c)
सदैव एक से अधिक
(d) एक के बराबर अथवा कम
Ans
d
3.
एक वस्तु प्रथम एक-तिहाई दूरी 20 मी/से के वेग
से, दूसरी एक-तिहाई
दुरी 30 मी/से के वेग से तथा अन्तिम एक-तिहाई दूरी 40
मी/से के वेग से तय करती है। औसत वेग लगभग होगा :
।
(a)
28 मी/से
(b)
38 मी/से
(c) 18 मी/से
(d)
8 मी/से
Ans
A
4.
एक वस्तु 10 किमी उत्तर की ओर तथा 20 किमी पूर्व की ओर जाती है। प्रारम्भिक स्थिति (initial point) से विस्थापन क्या होगा?.
(a)
22.36 किमी
(b)
2 किमी .
(c) 5 किमी .
(d) 20 किमी
Ans
A
5.
यदि समान घनत्व व भिन्न द्रव्यमान की दो गेंदें 100 मीटर की ऊँचाई से गिरायी जाती हैं, तब :
(a) दोनों पृथ्वी पर देर से
आयेंगी
(b) पहली गेंद पहले आयेंगी तथा
दूसरी उसके बाद
(c) दूसरी गेंद पहले आयेंगी तथा
पहली उसके बाद
(d) दोनों पृथ्वी पर साथ-साथ
आयेंगी ।
Ans
D
6.
एक कण का विस्थापन निम्न समीकरण द्वारा दिया गया है
y= a+bt +ct2– dt4 प्रारम्भिक वेग तथा त्वरण
क्रमशः हैं :
(a)
b, -4d
(b) - 5, 2c
(c)
5, 2c
(d)
2c, -4d
Ans
C
7.
किसी पिण्ड के त्वरण-विस्थापन वक्र के क्षेत्रफल से प्राप्त होता है
:
(a)
आवेग
(b) संवेग परिवर्तन प्रति एकांक
द्रव्यमान
(c) गतिज ऊर्जा में परिवर्तन
प्रति एकांक द्रव्यमान
(d) ऊर्जा में कुल परिवर्तन
Ans
C
8.
मन्दित (retarded) गति के लिये वेग-समय ग्राफ
का ढाल (slope) होता है :
(a)
शुन्य
(b)
ऋणात्मक
(c)
धनात्मक
(d)
धनात्मक या ऋणात्मक
Ans
B
9.
एक वस्तु विरामावस्था से 10 सेकण्ड के लिये 2
मी/से2 के त्वरण से गति प्रारम्भ
करती है, तत्पश्चात् 30 सेकण्ड के लिये
नियत चाल से चलती है और तब 4 मी/ से2 के मन्दन से विरामावस्था में आ जाती है। वस्तु द्वारा तय की गयी दूरी है
:
(a)
850 मीटर
(b) 750 मीटर
(c) 600 मीटर
(d)
इनमें से कोई नहीं
Ans
B
10.
एक कण को ऊध्र्वाधरतः ऊपर की ओर फेंका जाता है। इसका वेग क्या हो
जिससे कि यह 5 वें तथा 6 वें सेकण्ड
में समान दूरी तय करे :
(a)
48 मी/से
(b)
14 मी/से
(c) 7 मी/से
(d)
49 मी/से
Ans
D
11.
एक चोर की कार 10 मी/से की चाल से गतिशील है। 5
मी/से की चाल से इस कार का पीछा कर रही पुलिस की गाड़ी से एक गोली
चलाई जाती है, जिसका नालमुखी वेग (muzzle velocity)
72 किमी/घण्टा है। गोली किस चाल से कार से टकरावेगी?
(a) 10 मी/से
(b)
20 मी/से
(c) 15 मी/से
(d)
25 मी/से
Ans
C
for pdf notes download Suresh Lecturer App
https://play.google.com/store/apps/details?id=com.sureshlecturer
https://play.google.com/store/apps/details?id=com.sureshlecturer






























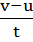



























Comments